メモリとは
メモリは、アプリやファイルを開いたときに一時的に保存される作業領域です。
コンピュータが行う計算などの処理はCPUが担い、必要なデータはディスクからロードしますが、計算前のデータや計算結果データは高速なメモリの領域を使用するのです。
メモリは主記憶装置というのが正式名称です。
最近ではUSBメモリもありますし、キャッシュメモリ(後術)もメモリの一部ではありますので、単に「メモリ」と言う場合は主記憶装置のことと認識しましょう。
メモリについて簡単な例で説明します。
ストレージには学生のテスト結果を計算する「アプリ」と、テスト結果の「データ」が格納されています。
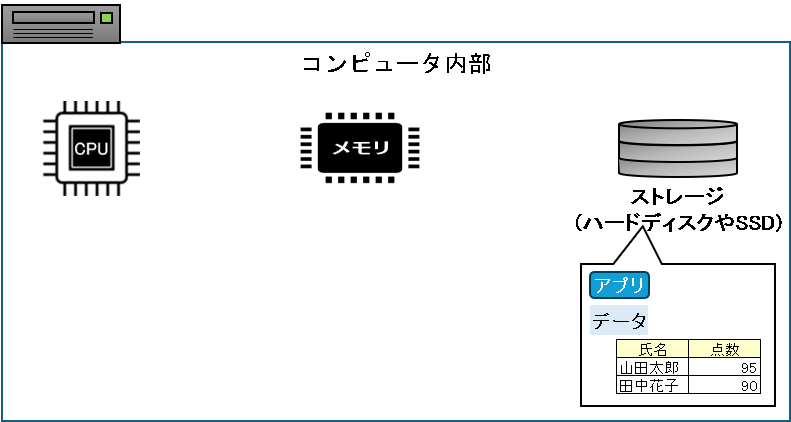
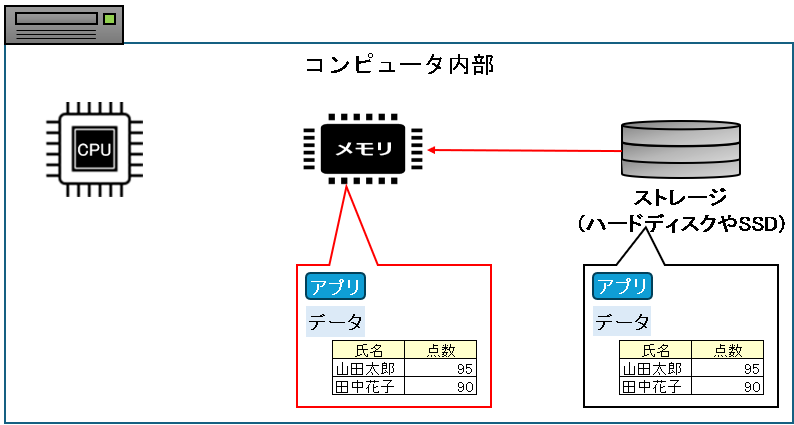
テスト結果から合計と平均を計算するために、アプリとデータをメモリに読み込みます。
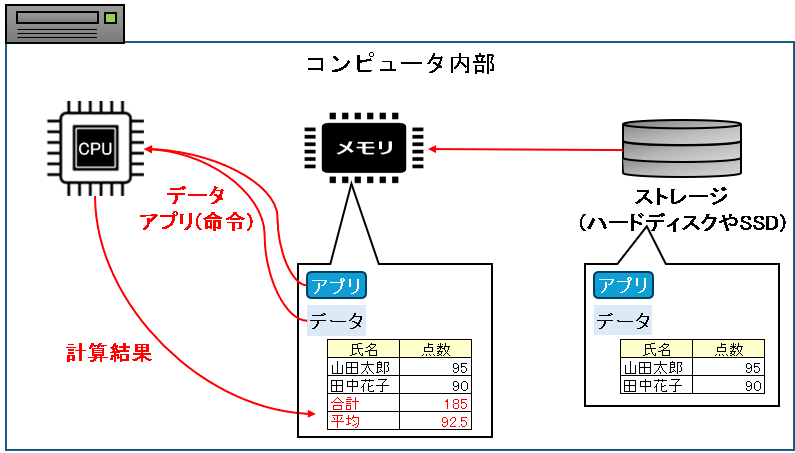
メモリに読み込んだアプリをデータをCPUに渡して計算結果をメモリに格納します。
メモリの種類:SRAMとDRAM
| 名称 | 速度 | 集積度 | 価格 | 用途 |
|---|---|---|---|---|
| DRAM | 遅い | 高い | 安い | メモリ(主記憶装置) |
| SRAM | 早い | 低い | 高い | キャッシュメモリ |
キャッシュメモリ
キャッシュメモリは、CPUとメモリ間のボトルネックを軽減する役割を果たしています。
昔のコンピュータは、キャッシュメモリがマザーボードに取り付けられることもありましたが、現在ではほとんどのキャッシュメモリはCPUの一部として統合されています。
キャッシュメモリの格納方式
フルアソシアティブ方式
フルアソシアティブ方式はキャッシュメモリに格納する場所を空いている領域に保管します。
空いている領域を順に探すので速度面で劣ります。
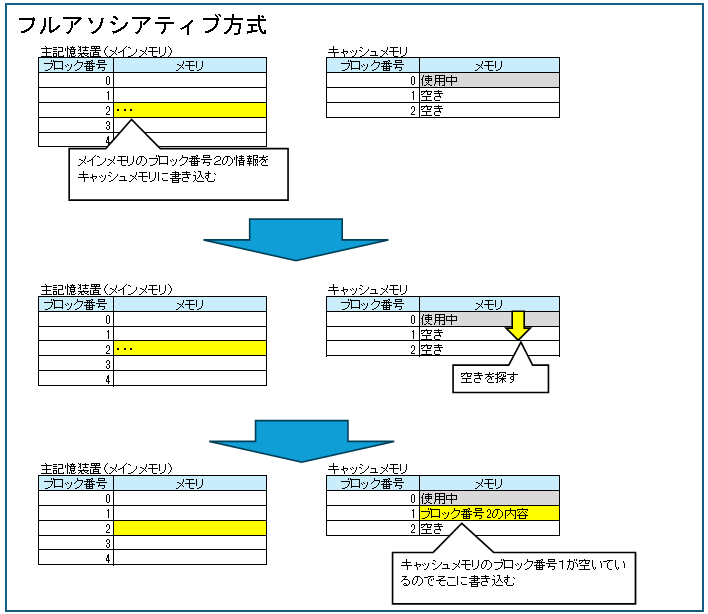
フルアソシアティブのキャッシュメモリ内の検索と格納の動きを詳細に説明します。
説明しやすいよう、シンプルにメモリが64バイトの例です。
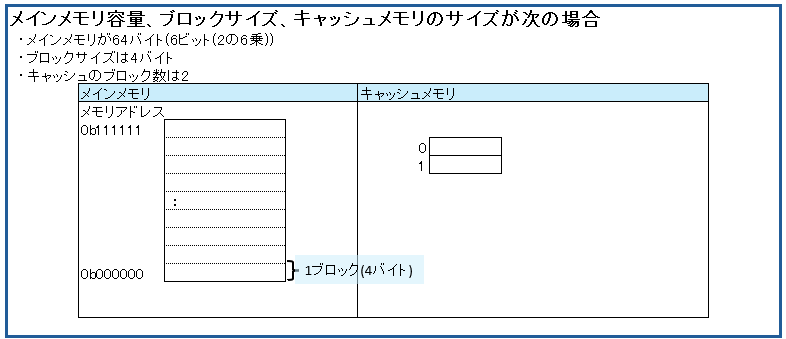
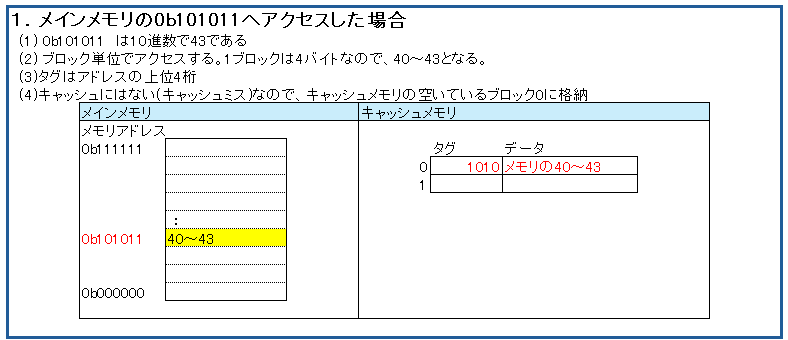
主記憶装置(メインメモリ)へアクセスしますが、キャッシュに存在しなかった(キャッシュミスだった)ので、キャッシュへ格納する場合の例です。
キャッシュの格納場所は空いている領域を使います。
キャッシュにはタグというメインメモリのアドレスの一部を格納して、後に検索(識別)用に使います。
続いて別の主記憶装置(メインメモリ)へアクセスし、キャッシュに存在した場合の例です。

ダイレクトマップ方式
ダイレクトマップ方式はキャッシュメモリの格納場所を計算で決めます。
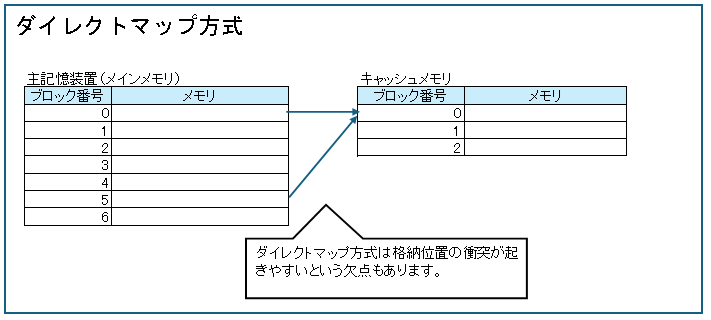
ダイレクトマップキャッシュメモリ内の検索と格納の動きを詳細に説明します。
説明しやすいよう、シンプルにメモリが64バイトの例です。
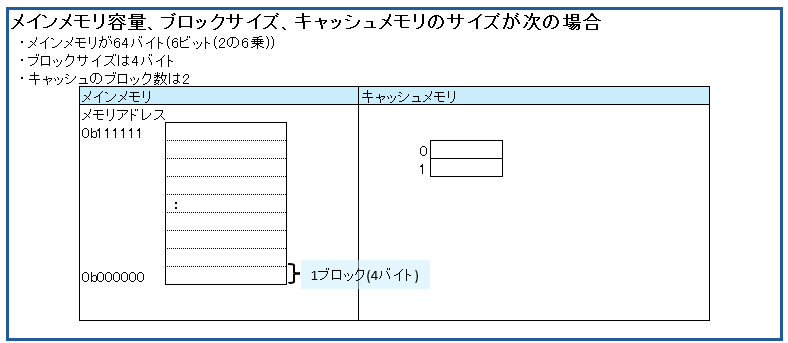
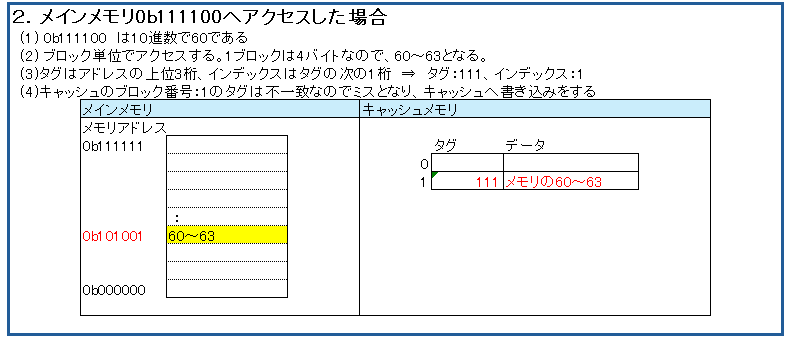
主記憶装置(メインメモリ)へアクセスしますが、キャッシュに存在しなかった(キャッシュミスだった)ので、キャッシュへ格納する場合の例です。
キャッシュの格納場所は、メインメモリのアドレスの一部をインデックス(=キャッシュのブロック番号)として使用して決定します。
キャッシュにはタグというメインメモリのアドレスの一部を格納して、後に検索(識別)用に使います。

続いて別の主記憶装置(メインメモリ)へアクセスし、キャッシュに存在しなかったので、上のキャッシュを上書きする場合の例です。
セットアソシアティブ方式
セットアソシアティブ方式は、キャッシュを複数の「セット」に分け、その中で順に探す仕組みです。
ダイレクトマップ方式とフルアソシアティブを組み合わせ方式です。
ダイレクトマップ方式と比べて、柔軟性が増します。
セットアソシアティブ方式のキャッシュメモリ内の検索と格納の動きを詳細に説明します。
説明しやすいよう、シンプルにメモリが64バイトの例です。
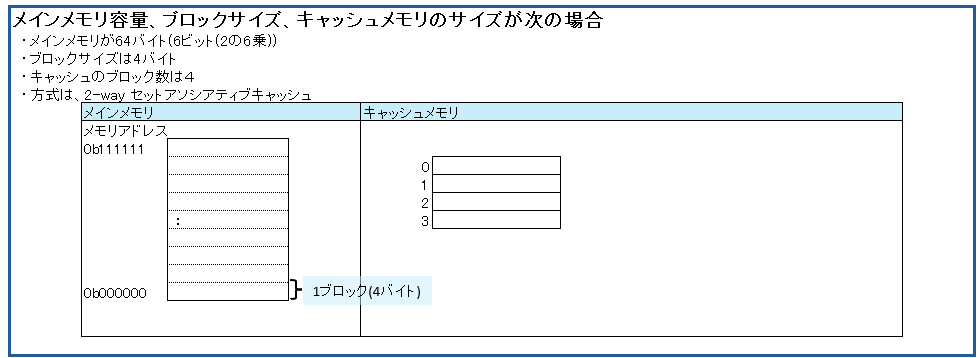
セットアソシアティブは、キャッシュメモリをセットというグループで分けます。今回の例は2wayなので2セットに分かれています。

主記憶装置(メインメモリ)へアクセスしますが、キャッシュに存在しなかった(キャッシュミスだった)ので、キャッシュへ格納する場合の例です。
キャッシュの格納場所は、メインメモリのアドレスの一部をインデックス(=キャッシュのブロック番号)として使用して決定します。
キャッシュにはタグというメインメモリのアドレスの一部を格納して、後に検索(識別)用に使います。

キャッシュメモリのアクセス時間
キャッシュメモリのアクセス時間が主記憶のアクセス時間の 1 / 30 で,ヒット率が95 % のとき,実効メモリアクセス時間は,主記憶のアクセス時間の約何倍になるか。
- 主記憶のアクセス時間をxとする。
- キャッシュメモリのアクセス時間は、1/30
- 実効メモリアクセス時間を求めます。(主記憶とキャッシュメモリを使った場合のアクセス時間)
・主記憶アクセス時間 : 1/30 × 0.95x
・キャッシュメモリアクセス時間 : (1 – 0.95)x
・実効アクセス時間は、主記憶アクセス時間 + キャッシュメモリアクセス時間なので
1/30 × 0.95x + (1 – 0.95)x
= 1/30 × 0.95x + x – 0.95x
≒ 0.081666x - よって、実効メモリアクセス時間は,主記憶のアクセス時間の約0.08倍です。



コメント