コンピュータが扱う情報「2進数」について
2進数は0と1だけで表現
コンピュータにデータや命令を伝える際は電気信号を使います。
電気信号は、電圧があるかないかで判断され、電圧がある場合は1、ない場合は0で表現します。

コンピュータは0と1だけで私たちが扱う数字、文字、画像、音などを処理しています。
なので、コンピュータの世界では1と0の羅列で情報を扱います。
コンピュータが扱う0と1だけの情報を「2進数」といいます。
私たちが普段使って言う数字は10進数といいます。
10になったら桁が増えるので10進数といいますが、2進数は2になったら桁が増えます。

ビット(Bit)とバイト
2進数で表現した場合、桁をビット(Bit)といいます。4桁であれば4ビット(Bit)、8桁であれば8ビット(Bit)です。
そして、8Bitは1バイト(Byte)と表現されています。
普段パソコンを使用しているときに、ファイルの容量を「1キロバイト(KB)」や「1ギガバイト(GB)」など「バイト」という単位をよく使いますが、この1バイトは8Bitに相当するのです。
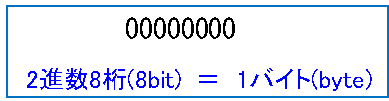
2進数の計算
2進数の足し算について説明します。
2進数の「0 + 1」は10進数と同じく1です。
2進数の0 + 1 ・・・ 0 + 1 = 1
続いて1 + 1 は桁が上がり10になります。
2進数の1 + 1 ・・・ 1 + 1 = 10
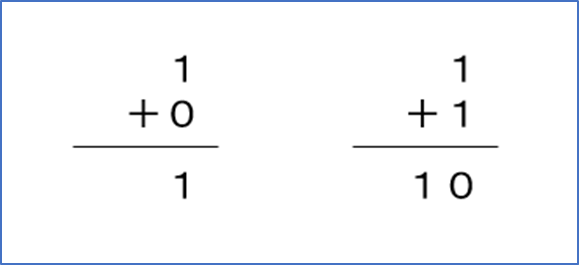
今度は2進数で101+111を計算してみます。
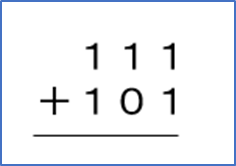
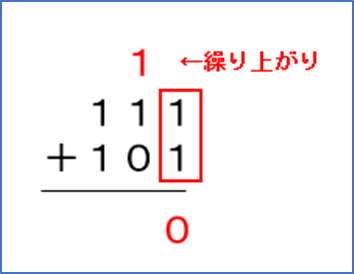
最初に1桁目(一番右の桁)を計算します。
1 + 1 = 0(繰り上がり1)
次に2桁目を計算します。
0 + 1 + 1 = 10(0を下に書き、1を繰り上げる)
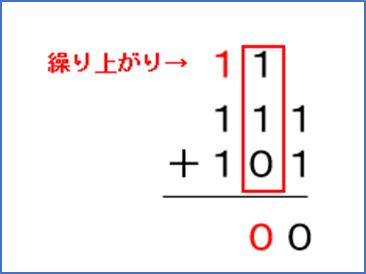
最後に3桁目を計算します。
1 + 1 + 1 = 11(1を下に書き、繰り上がりの1を次の桁に)
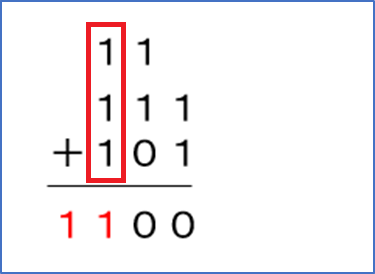
2進数⇔10進数の変換
コンピュータが扱う2進数と、普段私たちが使用している10進数は相互に変換できます。
2進数から10進数へ変換
2進数から10進数への変換は次の3ステップで求めることができます。
① まず、2進数は右の桁から順に2の1乗、2の2乗・・・と重みがあります。この重みを求めます。
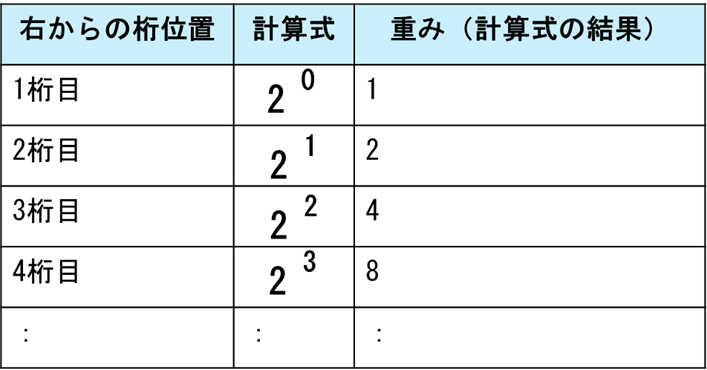
② 次にこの重みと、対応する桁の数字を掛けます。
③ 最後に結果を足します。
それでは2進数の「1001」を10進数に変換してみます。
①まずは各桁の重みを求めます。
右から4桁目は 2の3乗 ⇒ 8
右から3桁目は 2の2乗 ⇒ 4
右から2桁目は 2の1乗 ⇒ 2
右から1桁目は 2の0乗 ⇒ 1
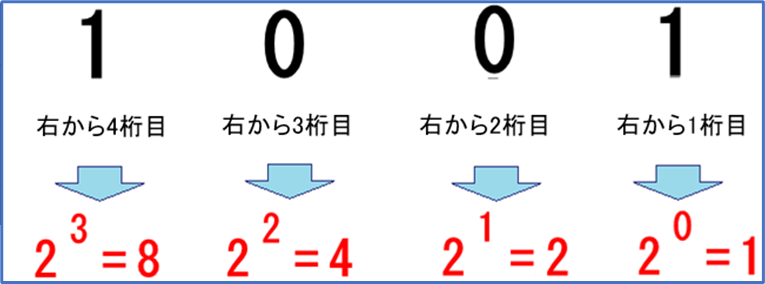
②次に求めた重みを、2進数の値と掛けます。
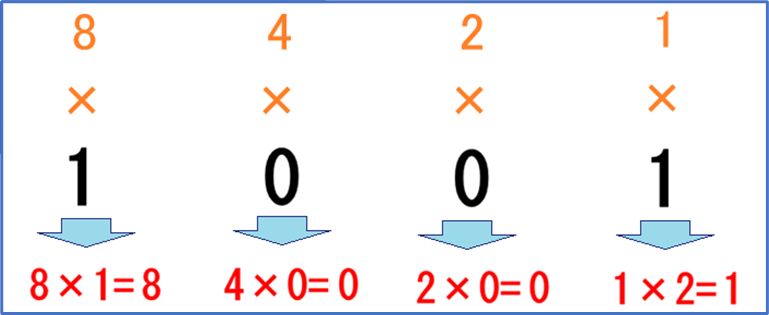
③ 最後に求めた数値をすべて足します。
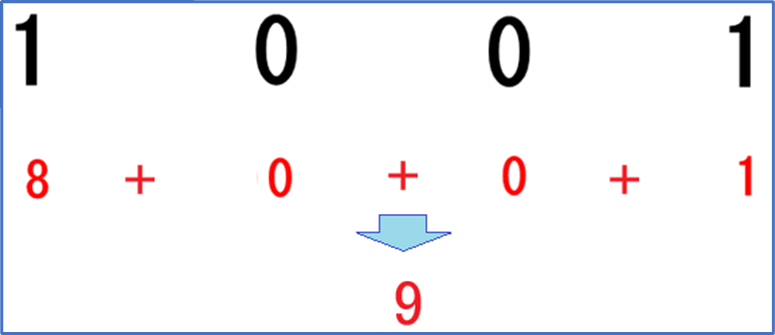
10進数から2進数へ変換
10進数から2進数へん関する手順は次の通りです。
① 10進数を2で割る
② 余りを記録
③ 上の商をさらに2で割り、同じことを商が0になるまで、繰り返す
この手順で10進数の「9」を2進数へ変換してみます。
① 9を2で割ります。その結果、余りは1で、商は4となりました。
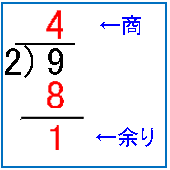
② 今度は先ほどの商を2で割ります。その結果、余りは0で商は2となりました。
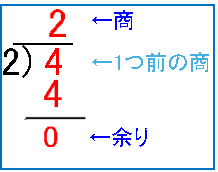
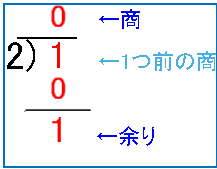
③ 同じように先ほどの商を2で割ります。その結果、余りは0で商は1となりました。
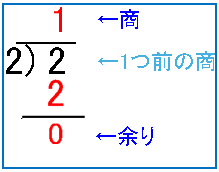
④ 同じように先ほどの商を2で割ります。その結果、余りは1で商は0となりました。
⑤ 商が0になったのでここで、今までのあまりを新しい結果順に左から並べます。
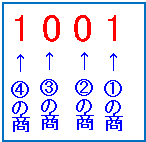
これで10進数から2進数への変換ができました。
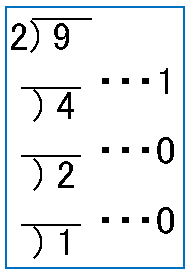
慣れてくると下のように、商と余りを連続して書いて、2進数を求めることができるようになります。
2進数における負の数(マイナス)を表す
2進数で負の数(マイナス)を表現することができます。
2進数で負の数(マイナス)を表現する方法として、プラスなのかマイナスなのかを符号を使って表すことです。
反転して1足すと負の数(マイナス)になる
本ページで説明してきた2進数は符号なしなので、負の数(マイナス)は表現できませんでした。
結論から言うと、符号ありの2進数の場合、負の数(マイナス)を表現する方法は「2進数を反転して1を足す」だけでよいのです。
例えば2進数「0001」は10進数にすると1です。これを反転すると「1110」となり1足すと「1111」になります。これが-1なのです。
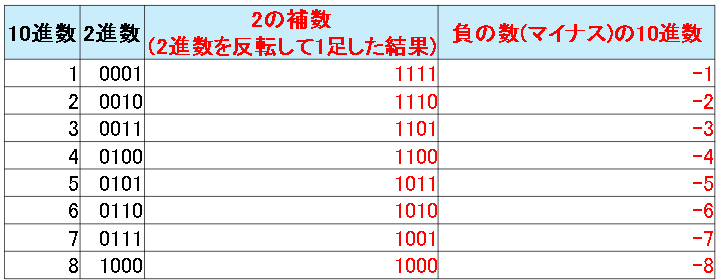
この反転して1を足した結果は「2の補数」といいます。
2の補数が負の数であることを確認してみる
2の補数で負の数を表現できる理由について解説します。
例えば、符号なし4Bitの2進数と、10進数との対応表は次の通りです。
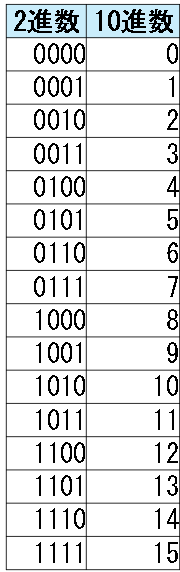
次に4bitを符号ありにした場合の10進数を追加します。
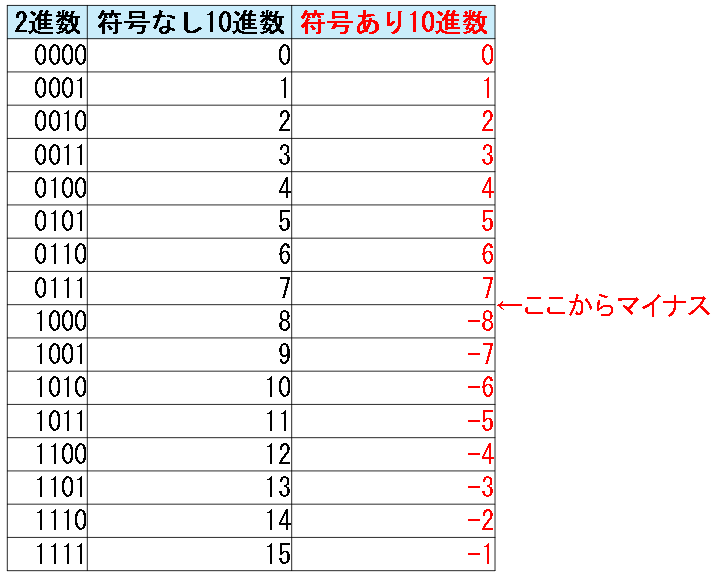
では、「-2 + 1」を計算してみます。
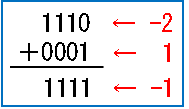
このように、2の補数を使って足し算すると、マイナスが考慮された引き算が実現でいきるのです。


コメント